効率的な情報の摂取について（１）：recallをrecallしない調査戦略

日々接する情報は多すぎる上に、まだ増加している。そのような情報過多(information overload)の問題に対して、precisionとrecallという２つの概念を参考に戦略を立ててみよう。

f:id:koshka-j:20171225005720j:plain

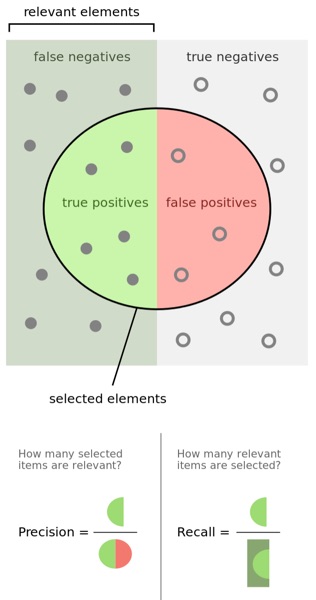
(画像：英Wikipediaの"Precision and Recall"より転載)

Precisionとrecallは、情報検索システム(例：Google)の「良さ」を測るために利用できる数値である。情報検索はinformation retrievalの訳語で、retrievalは「回収する行為」を表す名詞だ。

precisionは「システムが返した結果のうち、何割が実際に関連するものか」を測る数値だ。Googleで言えば、検索語に対して返された100万件の文書の中で、何件が検索語に関連するかを表す。式で表現すれば、 precision = (返却された要素のうち、関連する要素の総数) / (返却された要素の総数) という分数値になる。乱暴に言えばprecisionは日本語の「精度」や「質」にあたるだろう。

たとえばJobsでGoogle検索したとする。求職サイトではなくて、iPhoneの偉人に関連したサイトを返してほしい。Googleが返した100万件の文書のうち30万件がSteve Jobsに関連していれば、Precisionは 30万件 / 100万件 = 0.3 となる。100をかけてパーセンテージに単位変換すると30％だ。

recallはその逆で、「量」に目をつける。「この世の中に存在する全ての「関連するもの」のうち、システムはその何％を返したのか」というものだ（上掲の図を参照のこと）。実際には、何もかも検索対象に含めようとするとその間に人生が終わるので、1億文書とか100億文書とか十分に大きな値が「世の中に存在する全て」の近似として使われる。式で表現すれば、 recall = (返却された要素のうち、関連する要素の総数) / (システムが検索対象とする中で、関連する要素の総数) となる。

たとえばGoogle検索して100万件の文書が返って来たとする。先程の例と同様に、30万件の文書が検索語に関連していたと仮定し、更に全体で30億文書が関連していると仮定すると、 recall は 30万 / 30億 = 0.0001、すなわち0.01%である。precisionと比べると、分子は共通だが、分母が全く違うスケールの現象を捉えている。分母を変えるだけで「質」と「量」に似たものが測れるのは興味深い。

一般に質と量がトレードオフであるように、precisionとrecallは基本的にトレードオフの結果にある。たとえば100億文書全てを返せばrecallは1になるが、precisionはほぼゼロとなる。ほぼこれは確実だと思われる文書を１つだけ返せば、precisionは高確率で1になるが、recallはほぼゼロとなる。

ここまでが前置きである。PresicionとRecallが情報検索システムの良さを測るならば、人間の日々の情報摂取の良さの評価に使える。Googleに限らず、あらゆるメディアをチェックするとき、人間は情報検索システムであると言えるからだ。つまり私たち自体が、ろくに検索対象（e.g. 前例における100億文書）を広げる努力もせず、関連資料を見極めるスキルも身に着けないポンコツだと、良い情報など得られないということだ。Twitterで私たちが特定の人物をフォローするのは、その人が普段つぶやく内容のprecisionが高いからだ。TVをパッと付けてチャンネルを巡ったあとに電源を切ってしまうのは、その時間帯における precisionが 0 / チャンネル数 = 0 だったからだ。precisionがゼロだと一度確認した場合、あなたはその時間帯にTVをチェックすること自体をやめるだろう。そうして情報検索システムの性能を向上させる。

さて問題はinformation overloadだった。形式的に考えるための道具としてprecisionとrecallを手に入れたので、これらを参考にして改善策を考えてみる。

まず、どちらを使うと解決に近づくだろうか。

私は、recallは人間心理的に向いていないと主張する。世の中で私たちが「これは役立ちそうだ」「これ、いつか役立つから取っておこう」と思う文書は、恐らく億の単位で存在する。一方で、私たちが一日に確認できる文書は千の単位を超えないだろう。そうなるとrecallは先ほどと同じく最高でも 0.001%などと言った具合になる。どれだけ速読の訓練を積み、物事を一度聞いて瞬時に理解できるだけの把握力を持っていたとしても、このrecallは絶望的に低く、そして加速する全情報量の世界では今後も低下の一歩を辿る。微分値によってrecallが落ちていく速度の変化を調べることもできるが、だからどうしたという話だ。落ちていくrecallを何とかして遅くさせるのは『イシューからはじめよ』が説くところの犬の道であり、無駄に疲弊する。

precisionについては詳細な検証の価値がある。以下のシナリオを考えてみよう。

分厚い情報書籍を読む

たとえばある業界における２つの競合会社を比較した、ビジネス書を読むと決めたとする。この書籍の中から、あなたの情報検索システムは何を返すべきかを決める。残念ながらGoogleと異なり、書籍のページは読者が最も興味を持つ順によってソートされていることはない（そうなるように努める著者もいる）。よって読者は例えば以下の２つの読書戦略のうちどちらかを取る。

読書戦略１．ページを製本順に追っていく

簡単のため、書籍が300ページで、同一の長さの30の節によって構成されていたとしよう。つまり各節は10ページの長さだ。大抵の人は本をcover to coverで読む。そうすることによって、面白い節を見落とすミスをなくせる。

全てのページを読んだ場合、「(あなたという)システムが返した結果」は300ページとなる。仮に、30コの節のうち、18コの節があなたの興味に沿っていたとしよう。このときprecisionは180 / 300 = 0.6で60%となる。

読書戦略２．各節の見出しを見て、興味を持ったらそのページを読む

時間の節約を鑑み、節のタイトル（「株主構成の違い」や「設立経緯の違い」など）を見ることによって、あなたは20の節を読むことに決め、その中の14コを面白いと思ったとする。戦略１と比べると4コ見逃したわけであるが、あなたは20の節を読んだ段階で満足し、読書を終える。

このとき precisionは、(14*10) / (20*10) = .7 で70%となる。

この際、あなたはどちらの戦略を好むだろうか？

information overloadという時代背景を考えれば、僕は戦略２を好むだろう。precisionの高さもそうだが、読書時間の短さという魅力的なプレミアムも付いてくる。戦略２では、戦略１より高いprecisionを、2 / 3だけの時間で達成できている。多くの場合、情報摂取から得られる効用は、費やせる総自由時間量に制限される。パフォーマンスをprecision、コストを時間と考えたとき、戦略２は明らかに優れているといえる*1

現実を極端に単純化したこのシミュレーションには複数の反論が考えられる。一つ想定される反論は、recallを計算すると戦略１では驚きの100%、２では 14 / 18 = 77.7%であり、precisionとの(調和)平均を取ると戦略１の方が数値(F1値)が高くなるじゃないか、というものだ。だがF1はprecisionとrecallを等しく重んじた場合にたまたま計算される数値であり、現実において何の妥当性の根拠もない。Fβにおいてβ=1とおいただけの特殊な場合である。F0.5はprecisionを重んじ、F2はrecallを重んじる。加えて、繰り返すが、recallは年を追うごとに延々と下がり続けるのだ。重みの数字を毎年見直さなければいけないことになる。recallを入れた途端に、あなたはinformation overloadの時代の複雑性と真正面から向き合う犬の道に入る。

もしあなたがこのシミュレーションに何か惹かれるものを感じるならば、precision-orientedな情報摂取を意識的に試してみるのはどうだろうか。

上記では「読む節の選択」が十分に高速で、正確であることを前提している。あなたがその分野に不慣れで、20コの節を選んだときに面白いと思える節が3つしか含まれていなかった場合、precisionはむしろ下がる。だが投下した時間自体は短く押さえられているという利点はこれでも残る。

何より、その選択の精度を磨くこと自体も、実はinformation overloadへの有効な対策だとも考えられる。新しく使い始めたサービスの利用規約書、最近更新されたツイッターのプライバシーポリシー、授業で少し使っただけのプログラミング言語の分厚いマニュアル。全てに目を通している時間がないことは頻繁なのだ。

Deep Workをいま読んでいる最中なのだが、疑問を挟みたくなるような主張も多い。私はむしろこのprecision-based learningを可能にする情報フローとストックの方に興味がある。